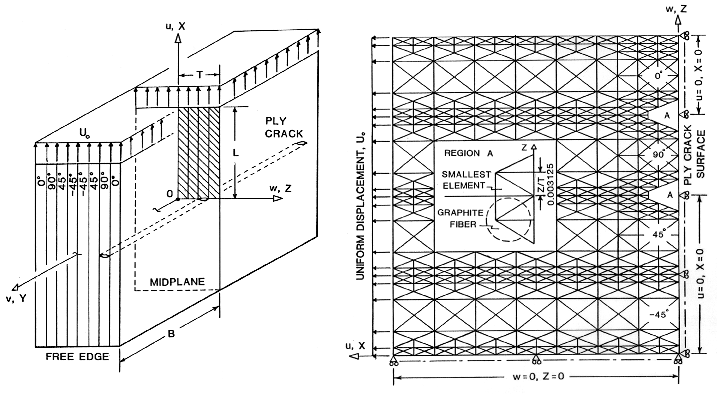
Figure 28. Schematic and FEM Grid of Ply Crack in a [0/90/+45/-45]s laminate
Ronald D. Kriz, Associate Professor
Engineering Science and Mechanics
Virginia Polytechnic Institute and State University
Blacksburg, Virginia 24061
After the formation of a ply crack, see Figure 25, new singularities occur near the ply crack tip. The growth of this crack can continue into the adjacent ply, see Figures 1, 3, 4, and 5, or debond along the interface. Below we provide models that demonstrate how anisotropy and residual stress can augment singularities near ply cracks and influence how ply cracks grow and control laminate fracture strength. In this section we provide:
Stress Analysis Summary: Details of the stress analysis is given in Reference [1]. Here we show a schematic of the laminate and finite element mesh that was used to model a ply crack in a [0/90/+45/-45]s laminate and the stress gradients ("concentrations") in the load bearing 0 degree ply near the ply crack tip, see also Figures 3 and 4.

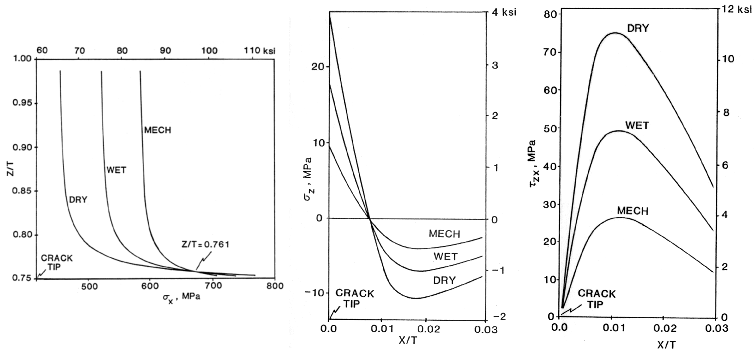
Summary: With the interactive computer program the reader can vary properties at the microscale and observe the effect these changes have on the stress distributions near the ply crack for two different types of quasi-isotropic laminates. Studying different laminates would require creating different FEM meshes. Future examples will target interactive FEM mesh generation. With this interactive computer program the reader can reproduce these results and study how variations on elastic properties and other properties at the microscale can influence the macroscopic stress state and influence laminate fracture.
Similar to the "Free-Edge" problem the model above predicts stress singularities of a ply crack in a eight-layered quasi-isotropic laminate. Below we introduce an FEM model for a simpler [0/90]s laminate with and without a woven macro-structure.