Problem Statement: Shape & Color Uniquely Define
Cijkl Anisotropy
The figures shown below are general geometric surface representations of
stress waves propagating through an anisotropic crystal.
There are actually three surfaces corresponding to the three eigenvalue
solutions to the Christoffel's equation but in this one special case
(orthorhomic symmetry) all three surfaces form a continuous connected surface.
For simiplicity we also show each of the three surfaces (eigenvalues
solutions) disconnected from the continuously connected surface.
THE SURFACES ARE SHOWN HERE ONLY AS AN EXAMPLE
YOUR SOLUTION CAN GENERTE SURFACES THAT CAN BE VERY DIFFERENT
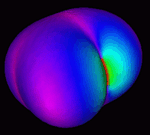
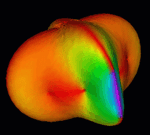
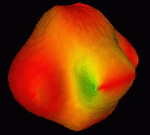

---- Outermost --------- Intermediate ------- Innermost -------- Combined -----
----- Fastest ------------ Slower ---------- Slowest ----- Connection Observed -
- Mostly Longitudinal -- Mostly Transverse -- Mostly Transverse -- with Translucency --
The directions of particle vibrations, [0 degrees (purple)] to 90 degrees (red)],
are the eigenvector solutions to the same equation. In the three-dimensional
surfaces we show a one-to-one mapping of eigenvectors (COLOR) onto their
corresponding eigenvalue surfaces (SHAPE).
The objective here is to observe the complete solution over the entire
three-dimensional region. SHAPE and COLOR are defined as solutions to
Christoffel's equation below. Geometric definitions for each term in the
Christoffel's equation and geometry of results are defined below.
Christoffel's Equation
Eigenvalue-Eigenvector Solutions Defined:
Eigenvector (Displacement Vibration Direction) Angles Defined:
Course content in this section: email
Dr. Ron Kriz
http://www.jwave.vt.edu/crcd/kriz/modules/module04/definitions.html
Created November 1997 / Modified January 1, 2001



