What is fracture toughness K_c?

Fracture toughness, K_c, is the resistance of a material to failure from fracture starting from a preexisting crack. This definition can be mathematically expressed by the following expression:

K_c = Y σ SQRT{π a}

Where Y is a dimensionless factor dependent on: the geometry of the crack and material, the loading configuration (i.e. if the sample is subject to tension or bending), and the ratio of crack length to specimen width, b. is the amount of load (stress) applied to the specimen, and a is the crack length.

Source Figures 1,2,3: Materials Science and Engineering: An Introduction, 3rd Edition, John Wiley & Sons, Inc. New York.

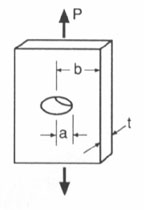
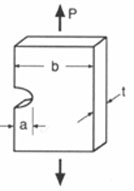
Figure 1 shows that a is not always the total length of the crack, but is sometimes half the crack length, as for an interior crack. The values for Y vary with respect to the shape and location of the crack. Some useful values of Y for short cracks subjected to a tension load are as follows:

Y = 1.00 For an interior crack similar to the crack shown in Figure 1

Y = 1.12 For a through-thickness surface crack as shown in Figure 2

Y = 0.73 For a half-circular surface crack as shown in Figure 3

Fracture toughness, K_c, has the English customary units of psi in^1/2, and the SI units of MPA m^1/2.

What is the plane strain fracture toughness, K_Ic?

For thin samples, the value K_c decreases with increasing sample thickness, b, as shown by Figure 4.

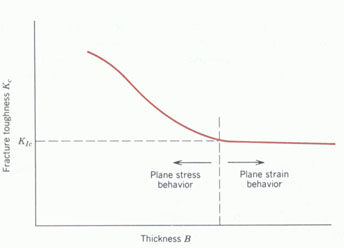
Ultimately, K_c becomes independent of b, at this point the sample is said to be under the conditions of plane strain. This fixed value of K_c becomes known as the plane strain fracture toughness, K_Ic. K_Ic is mathematically defined by:

K_Ic = Y σ SQRT{π a}

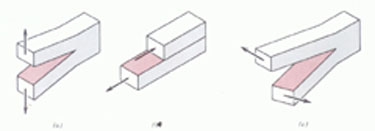
This value for the fracture toughness is the value normally specified because it is never greater than or equal to K_c. The I subscript for K_Ic, stands for mode I, or tensile mode, crack displacement as shown in Figure 5(a).

In general, K_Ic is low for brittle materials and high for ductile materials. This trend is supported by the K_Ic values in Table 1 (3,4).

Source: Materials Science and Engineering: An Introduction, 3rd Edition, John Wiley & Sons, Inc. New York.

How is K_Ic experimentally developed?

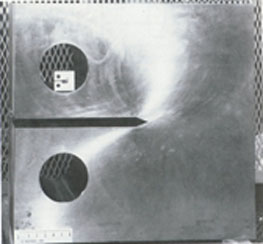
There are many different experiments which can be run in order to obtain a value for K_Ic. Almost any size and shape sample can be used, as long as it is consistent with mode I crack displacement. A possible, an rather simple, experiment that can be performed to find a value for K_Ic involves a sample, with known dimensions, similar to the one shown in Figure 6 and a screw-driven universal testing machine. This testing machine loads the specimen, at a constant strain rate, while a Load vs. Displacement curve is plotted by a X-Y recorder. From this plot, a possible value for can be calculated. With this value for , K_Ic can be calculated. For a more in depth explanation of this specific experiment, please refer to Experiment 6 in the Laboratory Manual for ESM 3060 (Prof. Duke) (5).

What is the effect of microstructure, temperature, thickness, and crack size and location on K_Ic?

As stated in the previous sections, many factors figure into the value of K_Ic for a given material. By definition (Equation 2), K_Ic varies with crack size and location, because crack size and location both factor into the value for a. As shown by Figure 4, K_Ic does not change with sample thickness. This non-variance is due to the condition of plane strain that the sample must be under to have a value for K_Ic. K_Ic does vary with temperature and strain rate.

It can be shown, by Figures 7 and 8, K_Ic increases with decreasing strain rate and increasing temperature. General strengthening methods, such as solid-solution hardening and strain hardening, tend to increase the samples yield stress, but these procedures commonly lead to a decrease in K_Ic. Additionally, K_Ic typically increases with decreasing grain size as composition and other microstructural variables are held constant (6,7,8).

Example Problem

1. If a support beam of 4340 Steel (tempered at 260 C) has an interior crack of length 5 mm, how much stress, σ, can be applied to it before it is expected to fracture?

Solution:

K_Ic = Y σ SQRT{π a}
50.0 MPa m^1/2 = 1.00 σ SQRT{π{5*10^-3}}         (2)
σ = 564 MPa

From Table 1, K_Ic for 4340 Steel (tempered at 260 C) is 50.0 MPa m^1/2. Then by knowing that Y = 1.00 for an interior crack, solve Equation 2 for σ.

Sources

1. Material Science and Engineering: An Introduction, 3rd Edition, William Calister, John Wiley & Sons, Inc. 1994, p. 193-195.

2. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue, Norman E. Dowling, Prentice Hall, 1993, p. 329 - 330.

3. Material Science and Engineering: An Introduction, 3rd Edition, William Calister, John Wiley & Sons, Inc. 1994, p. 194-196.

4. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue, Norman E. Dowling, Prentice Hall, 1993, p. 287-291.

5. ESM 3060 Laboratory Manual, Professor Duke, Virginia Polytechnic Institute and State University Copy Center.

6. Material Science and Engineering: An Introduction, 3rd Edition, William Calister, John Wiley & Sons, Inc. 1994, p. 193-195.

7. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue, Norman E. Dowling, Prentice Hall, 1993, p. 302-310.

8. Physical Metallurgy Principles, 3rd Edition, Robert E. Reed-Hill and Reza Abbaschian, PWS Publishing Company, 1994, p. 737-738.

Sources for the Figures

Figure 1. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue, Norman E. Dowling, Prentice Hall, 1993, p. 324.

Figure 2. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue, Norman E. Dowling, Prentice Hall, 1993, p. 301.

Figure 3. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue, Norman E. Dowling, Prentice Hall, 1993, p. 324.

Figure 4. Material Science and Engineering: An Introduction, 3rd Edition, William Calister, John Wiley & Sons, Inc. 1994, p. 194.

Figure 5. Material Science and Engineering: An Introduction, 3rd Edition, William Calister, John Wiley & Sons, Inc. 1994, p. 191.

Figure 6. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue, Norman E. Dowling, Prentice Hall, 1993, p. 304.

Figure 7. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue, Norman E. Dowling, Prentice Hall, 1993, p. 309.

Figure 8. Mechanical Behavior of Materials: Engineering Methods for Deformation, Fracture, and Fatigue, Norman E. Dowling, Prentice Hall, 1993, p. 311.

Table of Contents

Submitted by Matt McMurtry

Virginia Tech Materials Science and Engineering

http://www.eng.vt.edu/eng/materials/classes/MSE2094_NoteBook/97ClassProj/exper/mcmurtry/www/matt.html

Last updated: 4/25/97